EDA

Contents

Exploratory data analysis revealed some interesting trends in the data. We explore some of these trends below.

Imports

import requests
from IPython.core.display import HTML
styles = requests.get("https://raw.githubusercontent.com/Harvard-IACS/2018-CS109A/master/content/styles/cs109.css").text
HTML(styles)

from datetime import datetime

%matplotlib inline
import numpy as np
import pandas as pd
import matplotlib
import matplotlib.pyplot as plt
import seaborn as sns
sns.set(font_scale=1.5)
sns.set_style('ticks')
from sklearn.model_selection import train_test_split
from sklearn.ensemble import RandomForestClassifier

import warnings
warnings.filterwarnings('ignore')

EDA

loan_df = pd.read_pickle('./data/Pickle/clean_df_for_eda.pkl')
loan_df.shape

(1087436, 93)

Loan Amounts for Fully-Paid vs. Charged Off Loans

The plot below reveals that, on average, loans that end up being fully-paid are smaller (lower loan amount) than those that get charged off.

loan_df['Loan Outcome'] = loan_df['fully_paid'].map({1:'Fully Paid', 0: 'Charged Off'})

plt.subplots(figsize=(10,5))
plt.suptitle("Distribution of Loan Amounts for Fully-Paid vs. Charged Off Loans", x=.5, y=1.04).set_size(20)
sns.boxplot(x="loan_amnt", y="Loan Outcome", data=loan_df, palette='Set2'
           ).set(xlabel='Loan Amount (in dollars)', ylabel='');
plt.tight_layout()

png

Loan Outcome by Grade and Subgrade

Since we will be using the Lending Club’s assigned loan grades and subgrades in our model, we should assess whether these grades correspond to the borrower’s actual, observed delinquencies on the LC loan. Initial visualization below indicates that the LC loan grades and subgrades do correspond to the portion of loans fully paid; the portion of loans that get fully paid is higher for loans with less-risky loan grades.

Loan subgrade will likely be one of our model’s most important predictors, but we aim to refine our investment strategy by including additional features.

cols = ['grade', 'sub_grade']
labels = ['Loan Grade', 'Loan Subgrade']

fig, axes = plt.subplots(2,1,figsize=(12,12))
for i, ax in enumerate(axes):
    plt_data = loan_df.groupby(cols[i]).agg({'fully_paid': np.mean})
    #ax.set_title("Percentage of Loans that are Fully Paid by {}".format(labels[i]))
    sns.barplot(x=plt_data.index, y=plt_data['fully_paid'], ax=ax
             ).set(xlabel=labels[i],
                   ylabel='Portion of Loans Fully Paid')

fig.suptitle("Portion of Loans Fully Paid, by LC Grade and Sub-Grade", x=.5, y=1.02).set_size(20)
fig.tight_layout()

png

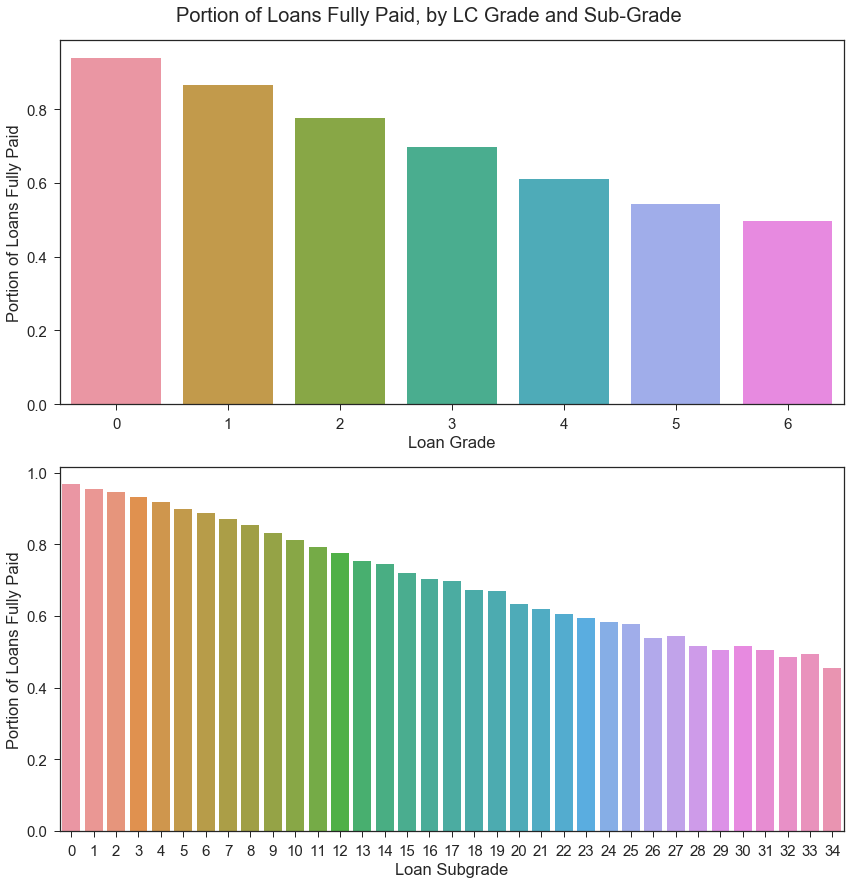
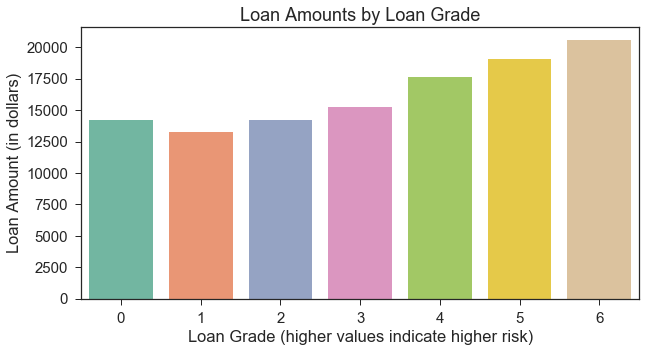
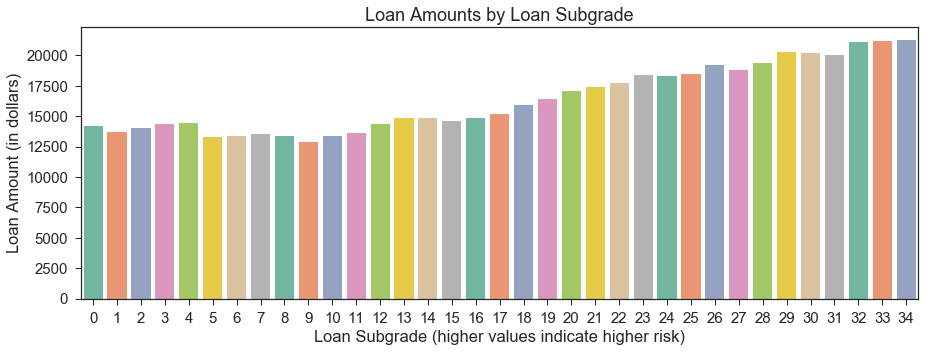
Loan Amount by Grade and Subgrade

Below, we observe that lower (less risky) grades/subgrades are associated with lower average loan amounts.

#Loan amount by grade
group = loan_df.groupby("grade").mean()
avg_loan = group['loan_amnt'].reset_index()
xticklabels = avg_loan.index.tolist()

plt.subplots(figsize=(10,5))
plt.title("Loan Amounts by Loan Grade")
sns.barplot(x='grade', y='loan_amnt', data=avg_loan, palette='Set2'
           ).set(xlabel='Loan Grade (higher values indicate higher risk)', ylabel='Loan Amount (in dollars)',
                 xticklabels=xticklabels);

png

#Loan amount by sub_grade
group = loan_df.groupby("sub_grade").mean()
avg_loan = group['loan_amnt'].reset_index()
plt.subplots(figsize=(15,5))
plt.title("Loan Amounts by Loan Subgrade")
sns.barplot(x='sub_grade', y='loan_amnt', data=avg_loan, palette='Set2'
           ).set(xlabel='Loan Subgrade (higher values indicate higher risk)', ylabel='Loan Amount (in dollars)');

png

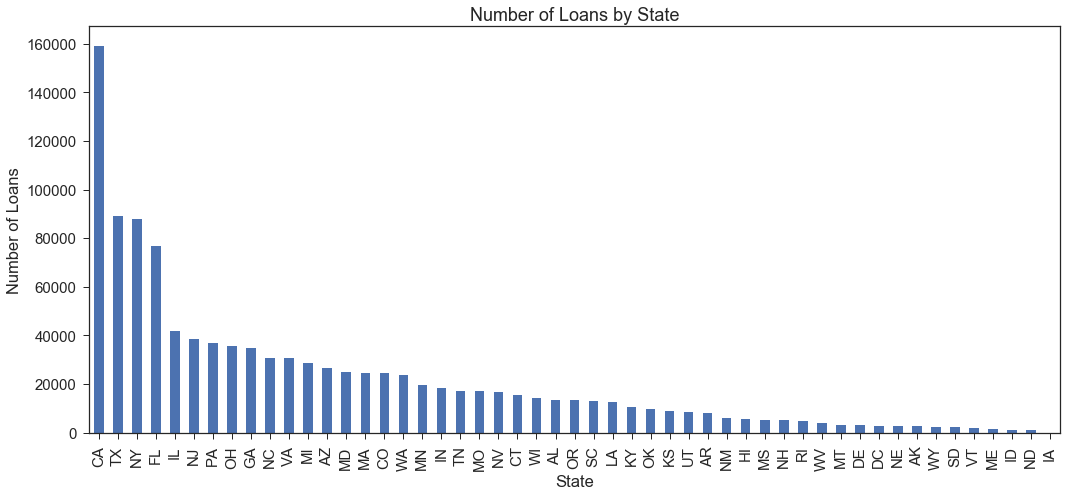
Number of Loans in Dataset by State

Below, we see that a large number of loans are issued to borrowers in California, Texas, New York, and Florida relative to the number of loans issued in other states. We may compare loan performance by state, but we should ensure that our investment strategies do not discriminate based on a borrower’s state.

loan_origin=pd.DataFrame(loan_df.groupby('addr_state')['addr_state'].agg('count').sort_values(ascending=False))
loan_origin.plot(kind='bar', figsize=(15,7), legend=False)
plt.xlabel('State')
plt.ylabel('Number of Loans')
plt.title('Number of Loans by State')
plt.tight_layout()

png

adress_loan = ['addr_state', 'Loan Outcome']
cm = sns.light_palette("green", as_cmap=True)
pd.crosstab(loan_df[adress_loan[0]], loan_df[adress_loan[1]]).style.background_gradient(cmap = cm)
Loan Outcome Charged Off Fully Paid
addr_state
AK 531 2115
AL 3306 10267
AR 1998 6106
AZ 5265 21386
CA 31475 127662
CO 3755 20591
CT 2731 12750
DC 374 2346
DE 622 2400
FL 16524 60113
GA 6438 28355
HI 1139 4463
IA 1 1
ID 229 965
IL 7770 33866
IN 3958 14320
KS 1527 7590
KY 2281 8218
LA 3010 9609
MA 4761 19722
MD 5371 19644
ME 203 1230
MI 5851 22925
MN 3983 15602
MO 3647 13411
MS 1364 3913
MT 542 2577
NC 6432 24425
ND 256 905
NE 675 2027
NH 737 4478
NJ 8278 30268
NM 1306 4773
NV 3675 12890
NY 19700 67985
OH 7651 27915
OK 2409 7514
OR 1949 11579
PA 7825 28947
RI 844 3832
SC 2114 10755
SD 491 1769
TN 3702 13469
TX 17845 71410
UT 1445 6904
VA 6305 24438
VT 298 1826
WA 3731 20152
WI 2524 11741
WV 673 3365
WY 430 1971

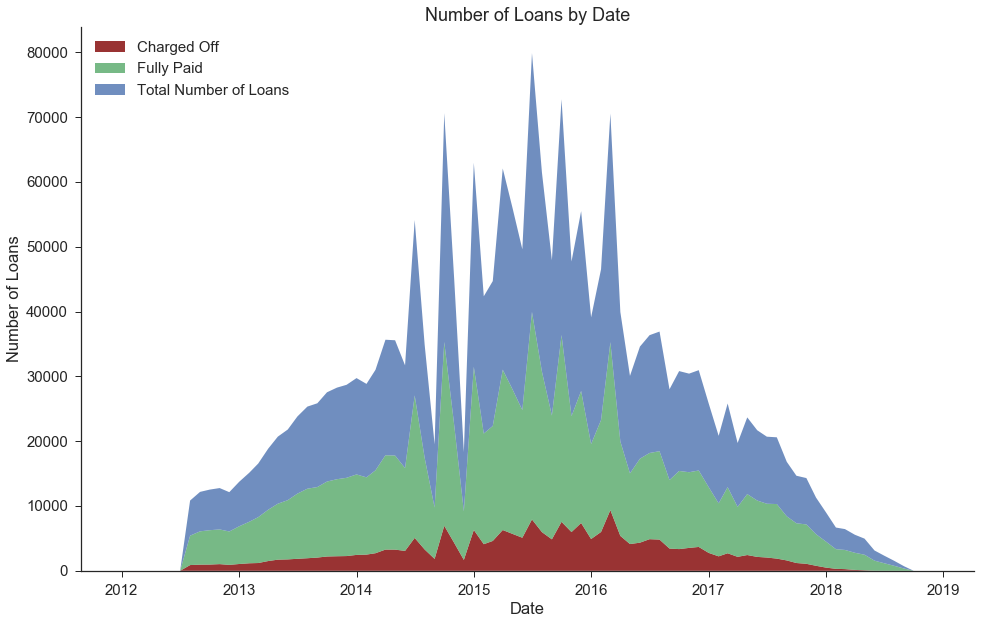
Number of Fully Paid vs. Charged Off Loans by Date of Loan Issuance

We observe that there are fewer loans in our dataset from the more recent dates. This is not because the overall number of Lending Club loans has decreased recently, but rather because we only selected loans that have been completed (either fully paid or charged off, rather than those that are still in progress).

dates = []
total_loans = []
fully_paid = []
charged_off = []

for year in range(2012,2019):
    for month in range(1,13):
        tmp = loan_df[loan_df['issue_d']==datetime(year,month,1)]
        dates.append(datetime(year,month,1))
        total_loans.append(tmp.shape[0])
        fully_paid.append(tmp[tmp['Loan Outcome']=='Fully Paid'].shape[0])
        charged_off.append(tmp[tmp['Loan Outcome']=='Charged Off'].shape[0])

fig, ax = plt.subplots(figsize=(16,10))

plt.stackplot(dates,[charged_off,fully_paid,total_loans], 
              labels=['Charged Off','Fully Paid','Total Number of Loans'], 
              alpha=0.8,colors=['#800000', '#55a868', '#4c72b0'])


ax.set_title('Number of Loans by Date')
ax.set_xlabel('Date')
ax.set_ylabel('Number of Loans')
plt.legend(loc='upper left')

sns.despine();

png

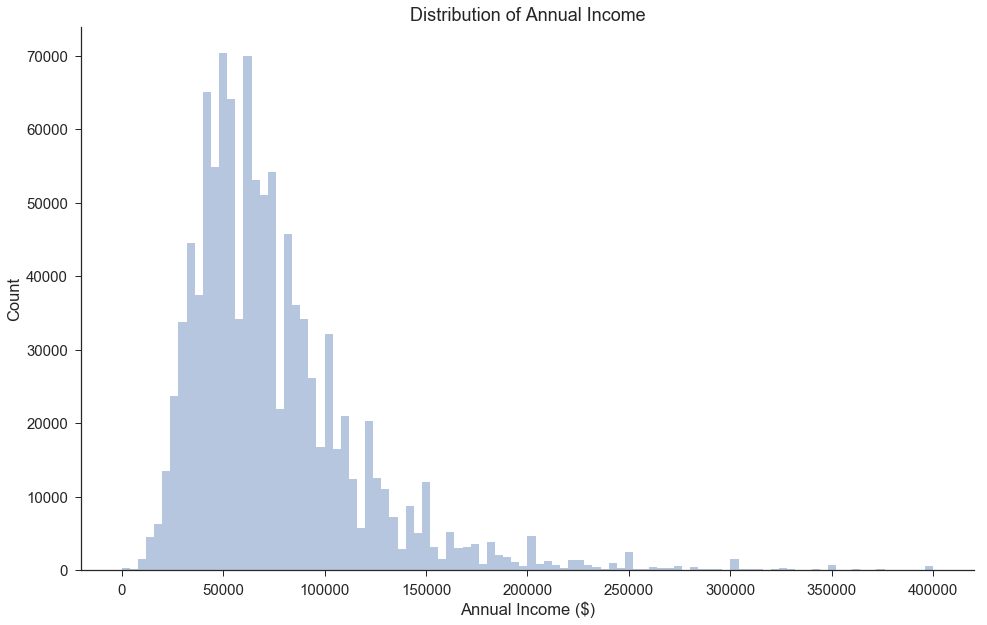
Distribution of Annual Income

We observe that a large portion of the Lending Club loans have applicants who have incomes of around 50k to 70k per year.

There appear to be loans issued to borrowers with very low income, including incomes of 0. This group may include students and people who have recently lost their jobs or had employment changes. It is also possible that these borrowers had co-signers.

fig, ax = plt.subplots(figsize=(16,10))

sns.distplot(loan_df[loan_df['annual_inc']<=400000]['annual_inc'],bins=100,kde=False,rug=False)

ax.set_title('Distribution of Annual Income')
ax.set_xlabel('Annual Income ($)')
ax.set_ylabel('Count')

sns.despine();

png

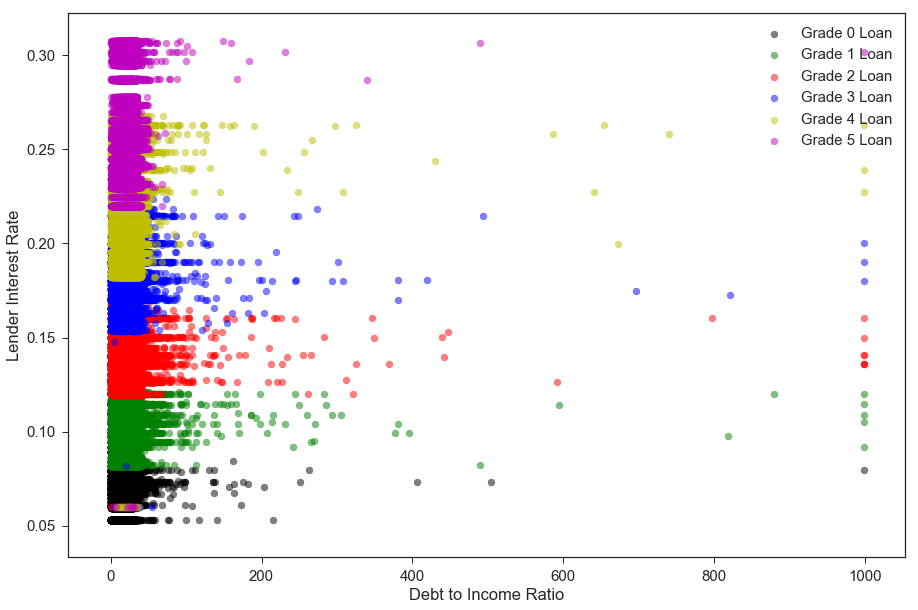
Borrower’s Debt-to-Income Ratio vs. Lending Club Interest Rate (by Loan Grade)

Our main conclusion from the plot below is that there is a clear-cut relationship whereby riskier-grade loans have higher interest rates. Upon further investigation, we found that the “Lending Club’s interest rates take into account credit risk and market conditions”(Source: https://www.lendingclub.com/foliofn/rateDetail.action). The interest rate is assigned directly based on the loan subgrade and the current market conditions.

Riskier applicants also tend to have higher debt-to-income ratios, though the visualization below does not portray this as clearly.

loan_df['interest_rate']=loan_df['int_rate']

#Interest Rates change over time. Let's look at 2018Q2 only.
tmp_df = loan_df[(loan_df['issue_d']>=datetime(2018,4,1))|(loan_df['issue_d']<datetime(2018,7,1))]
#tmp_df['grade'] = tmp_df['grade'].astype('category')

colors=['k','g','r','b','y','m','c']
counter=0
fig, ax = plt.subplots(1, 1, figsize=(15, 10))

for grade in np.sort(tmp_df['grade'].unique()[0:-1]):
    ax.scatter(tmp_df[tmp_df['grade']==grade].dti, tmp_df[tmp_df['grade']==grade].interest_rate, alpha=0.5, color=colors[counter], label='Grade '+ str(grade)+ ' Loan')
    counter+=1

ax.set_xlabel('Debt to Income Ratio')
ax.set_ylabel('Lender Interest Rate')
ax.legend(loc='best');

png

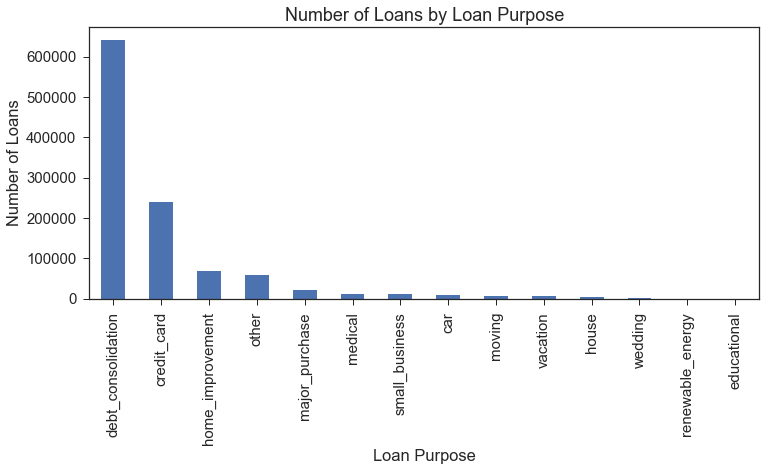
Loan Purpose Distribution

The purpose of the large majority of the loans is categorized as debt consolidation, with credit card debt being the next-most common loan purpose.

These categories likely include many individuals who have low incomes but expect to have higher incomes in the near future, including students or younger applicants who have recently joined the work force.

fund_purpose=pd.DataFrame(loan_df.groupby('purpose')['purpose'].agg('count').sort_values(ascending=False))
fund_purpose.plot(kind='bar', figsize=(12,5), legend=False)
plt.xlabel('Loan Purpose')
plt.ylabel('Number of Loans')
plt.title('Number of Loans by Loan Purpose');

png

Removing Excess Columns

The following columns were already re-coded into dummy variables, and we only kept the original columns to facilitate EDA visualizations: application_type, emp_length, home_ownership, purpose, term, verification_status]

We also drop the columns we temporarily generated for visualization purposes: Loan Outcome and interest_rate

columns = ['application_type', 'emp_length', 'home_ownership', 'purpose', 'term',
           'verification_status', 'Loan Outcome', 'interest_rate']

loan_df = loan_df.drop(columns=columns)

loan_df.shape

(1087436, 87)

loan_df.to_pickle('./data/Pickle/clean_df.pkl')

Random Forest Feature Importances

Since our full dataset is so large, we use a 10% sample of our dataset for the purposes of tuning and comparing baseline models.

We still have a large number of potential features, and we would like to get a sense of which features are most useful in predicting the loan outcome. We train a Random Forest Classifier and use the feature importances to select the top features.

We specifically set max_depth=None to allow for all features to be incorporated.

clean_df = pd.read_pickle('./data/Pickle/clean_df.pkl').sample(frac=.10, random_state=0)
clean_df = clean_df.drop(columns= ['issue_d', 'zip_code', 'addr_state'])
outcome='fully_paid'

data_train, data_val = train_test_split(clean_df, test_size=.1, stratify=clean_df[outcome], random_state=99);

X_train = data_train.drop(columns=outcome)
y_train = data_train[outcome]

X_val = data_val.drop(columns=outcome)
y_val = data_val[outcome]

#Train random forest, allowing overfitting
rf_model = RandomForestClassifier(n_estimators=100, max_depth=None).fit(X_train, y_train)

importances = pd.DataFrame({'Columns':X_train.columns,'Feature_Importances':rf_model.feature_importances_})
importances = importances.sort_values(by='Feature_Importances',ascending=False)
importances.head(20)

fig, ax = plt.subplots(figsize=(12,50))
ax = sns.barplot(x=importances['Feature_Importances'], y=importances['Columns'])
sns.despine()

png